Split Cell capability to FixedComp

Within many objects either internal or external cells can become excessively complex. This is often because a simple cell has multiple excludes added to it. In MCNP or PHITS this is normally not a problem but for FLUKA it is fatal.

There are two new methods to produce a split cell within CombLayer: SplitObject and ContainedSpace. Both can produce the same results, and both can be used in place of each other, but depending on the situation one is normally an easier and quicker choice than the other.

ContainedSpace is best used when there is a large volume that needs to be sliced linearly into segments. E.g a beamline composed of many components will leave the hutch / cave or space it resides in as a very complex cell. If that beamline is linear (e.g. A - B -C with each piece linking the the tail of the previous one) then ContainedSpace is an ideal system. ContainedSpace is not designed to readily deal the component that the space spaces overlap each other e.g. a beam line with a sample in the centre and multiple detector banks radially arranged round the sample.

SplitObject is designed for cases were a volume can be divided into region A and region B were the complexity of A and B is expected to be similar (but less than the initial region).

Consider the Balder beam line as an example:

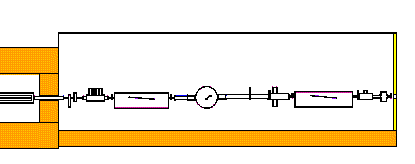
The beam line has a hutch with multiple complex components mostly linearly arranged (e.g. one after the other). The void space is far too complex for use with FLUKA.

ContainedSpace is then used to split each components volume from each other. ContainedSpace is inherited from ContainedComp so should be used instead of ContainedComp in an object that can be split [or may have that possibility].

If the user does not need the splitting capacity then use the object in the normal way, and no action is taken. The normal addInsertCell and other features of a ContanedComp work as expected.

If a region needs to be removed, the simplest way is to register two link points of the object with the command like:

ObjectPtr->registerSpaceCut(1,2);

This goes before the createAll command, e.g.

gateE->addInsertCell(Hutch->getCell("Void"));
gateE->setFront(*pipeG,2);
gateE->registerSpaceCut(1,2);
gateE->createAll(System,*pipeG,2);

Here we see a gateE object being created. First the gate is put into the hutch void (as normal for ContainedComp), it has a link point set (back of pipeG) and then the registerSpaceCut of two values 1,2 [these must be different].

The createAll then builds the whole object and calls createLinks (internally) and finally call ContainedSpace::insertCell which split the volume by creating a volume bound by the internal direction of those two link points. The volume is then excluded from Hutch void cell, and the gate is placed within this new void volume.

The internal code constructs the local void volume by extending lines from either link point that are orthogonal to the link axes. Any surface NOT found in that process are removed from the original Hutch Void to make the new local void. Additional non-found surfaces can be added if needed [typically for bridging surfaces on cylinders/sphere etc]

If the internal link points are not correct then ANY link point can be used, even to the point of constructing a new one explicitly for this problem. This is particularly useful when an object leave/enters a volume as the link surface on the boundary of the Hutch void can be used instead. If for example, the user wished to set the first link point to the hutch inner surface, the command might be:

gateE->setSpaceLinkCopy(0,*Hutch,Hutch->getSideIndex("-innerFront"));
gateE->registerSpaceCut(0,2);
gateE->createAll(System,*pipeG,2);

This sets the 0 link point to be a copy of Hutch's innerFront link point. Note that registerSpaceCut is set to 0,2 because we don't want to overwrite the link point.

More examples are given in test/testContainedSpace.cxx

Shows a beamline with ContainedSpace section divisions

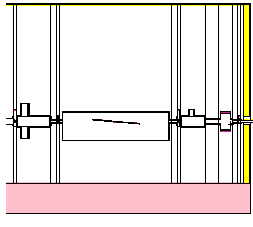
The volume here has been divided multiple times by each of the ContainedSpace objects. The sub-volume sections are different lengths but in principle they have the same algebraic complexity.

Note in this case the whole hutch void cell was tiled by ContainedSpace units so a

System.removeCell(Hutch->getCell("Void"));

command was given at the end of the sequence to tidy up the space. [The model would still work but the Hutch Void cell would be a redundant zero volume space].